Khám Phá Cách Tính Hệ Nhị Phân Trong Tin Học

Trong kỷ nguyên công nghệ số ngày nay, việc hiểu và nắm vững hệ nhị phân là một điều không thể thiếu đối với những ai đam mê lĩnh vực tin học. Mặc dù có vẻ đơn giản với chỉ hai chữ số 0 và 1, hệ nhị phân lại là nền tảng chính để máy tính có thể thực hiện các tính toán phức tạp, xử lý dữ liệu và điều khiển các quá trình. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tính hệ nhị phân trong tin học, bao gồm các khái niệm cơ bản và ứng dụng của nó trong thế giới số.

Cách Tính Hệ Nhị Phân Trong Tin Học

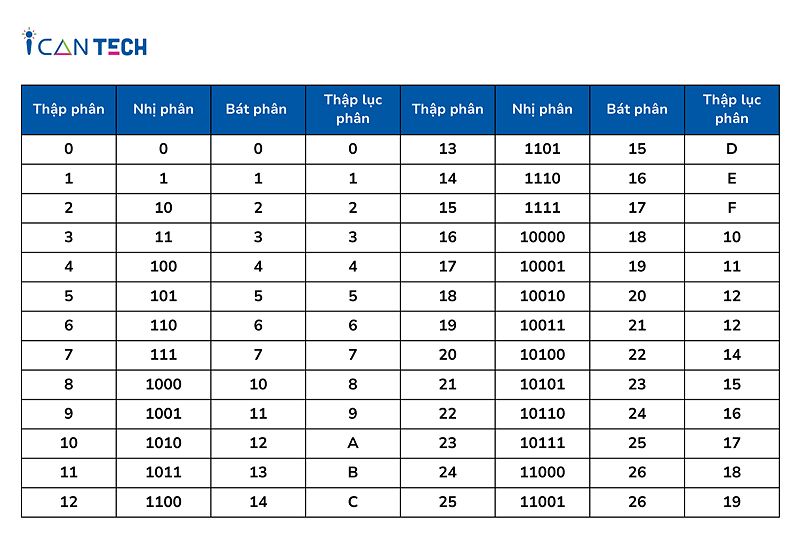
Trong hệ nhị phân, mỗi chữ số (hay bit) chỉ có thể nhận hai giá trị là 0 hoặc 1. Tuy đơn giản, nhưng cách thức biểu diễn số lại rất quan trọng để máy tính có thể hiểu và xử lý thông tin.

Giá trị của một số nhị phân được xác định dựa trên vị trí của các bit, tương tự như trong hệ thập phân chúng ta thường dùng. Cụ thể:

Bit ở vị trí đầu tiên (bên phải) có giá trị 2^0 = 1.
Bit ở vị trí thứ hai có giá trị 2^1 = 2.
Bit ở vị trí thứ ba có giá trị 2^2 = 4.
Và cứ như vậy, mỗi vị trí bit sẽ tăng gấp đôi so với vị trí bên phải.

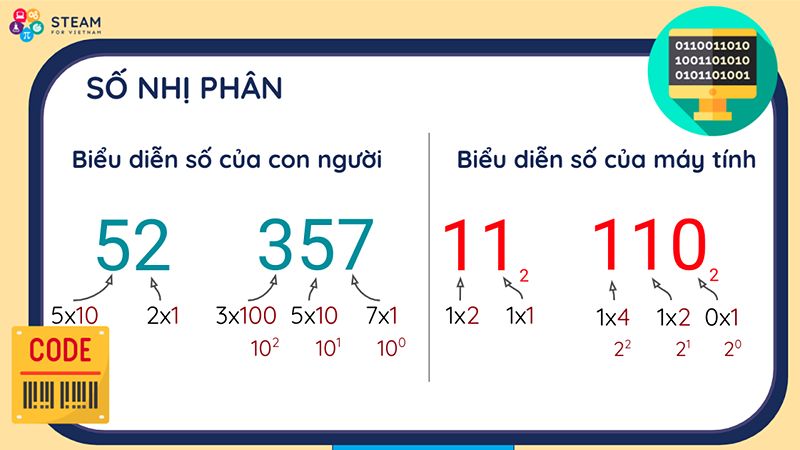
Ví dụ, số nhị phân 101101 có giá trị tương đương với:

(1 × 2^5) + (0 × 2^4) + (1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) = 32 + 0 + 8 + 4 + 0 + 1 = 45 (hệ thập phân)

Chuyển Đổi Giữa Hệ Thập Phân và Hệ Nhị Phân

Việc chuyển đổi giữa hai hệ số này là một kỹ năng quan trọng mà bạn cần nắm vững. Hãy cùng tìm hiểu cách thực hiện các phép chuyển đổi này.

Chuyển Đổi Từ Thập Phân Sang Nhị Phân

Để chuyển một số thập phân sang hệ nhị phân, bạn thực hiện theo các bước sau:

Chia số thập phân đó cho 2, ghi lại phần dư.
Chia kết quả thu được ở bước 1 tiếp cho 2, ghi lại phần dư.
Lặp lại bước 2 cho đến khi kết quả chia bằng 0.
Các phần dư được ghi lại theo thứ tự từ dưới lên sẽ cho ta số nhị phân tương ứng.

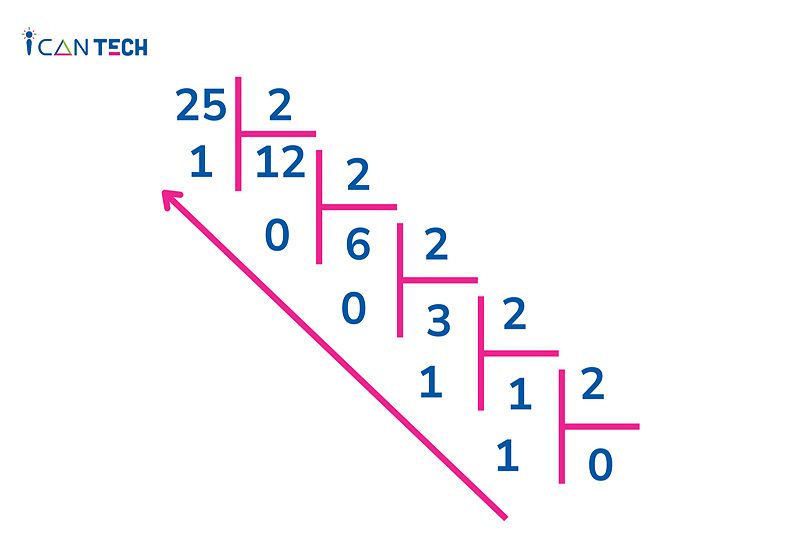
Ví dụ, chuyển số 45 (thập phân) sang hệ nhị phân:

45 ÷ 2 = 22, dư 1 22 ÷ 2 = 11, dư 0 11 ÷ 2 = 5, dư 1 5 ÷ 2 = 2, dư 1 2 ÷ 2 = 1, dư 0 1 ÷ 2 = 0, dư 1

Vậy số 45 (thập phân) tương đương với 101101 (nhị phân).

Cach-chuyen-doi-he-nhi-phan-sang-thap-phan

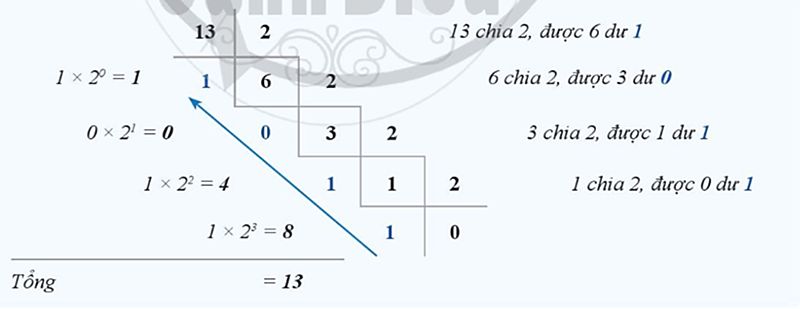
Chuyển Đổi Từ Nhị Phân Sang Thập Phân

Ngược lại, để chuyển một số nhị phân sang hệ thập phân, bạn thực hiện như sau:

Nhân từng bit với giá trị tương ứng của nó (2^0, 2^1, 2^2, …).
Cộng tất cả các kết quả lại.

Ví dụ, chuyển số nhị phân 101101 sang hệ thập phân:

(1 × 2^5) + (0 × 2^4) + (1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) = 32 + 0 + 8 + 4 + 0 + 1 = 45

Vậy số nhị phân 101101 tương đương với số thập phân 45.

Chuyen-doi-thap-phan-sang-nhi-phan

Các Phép Toán Bit Cơ Bản

Ngoài việc biểu diễn và chuyển đổi giữa các hệ số, hệ nhị phân còn cho phép thực hiện các phép toán bit cơ bản như:

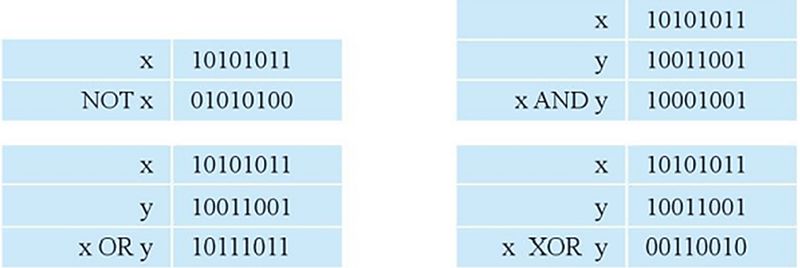
Phép NOT (Phép Bù)

Phép NOT là phép toán một ngôi, cho kết quả ngược lại với giá trị đầu vào. Cụ thể:

NOT 0 = 1
NOT 1 = 0

Ví dụ: NOT 10101 = 01010

Phép AND (Phép Nhân Logic)

Phép AND là phép toán hai ngôi, cho kết quả 1 khi cả hai bit đầu vào đều là 1, và 0 trong các trường hợp còn lại.

Ví dụ: 10101 AND 11001 = 10001

Phép OR (Phép Cộng Logic)

Phép OR là phép toán hai ngôi, cho kết quả 0 khi cả hai bit đầu vào đều là 0, và 1 trong các trường hợp còn lại.

Ví dụ: 10101 OR 11001 = 11101

Phép XOR (Phép Hoặc Loại Trừ)

Phép XOR là phép toán hai ngôi, cho kết quả 1 khi hai bit đầu vào khác nhau, và 0 khi chúng bằng nhau.

Ví dụ: 10101 XOR 11001 = 01100

Các phép toán bit này là nền tảng cho việc thực hiện các phép tính toán và xử lý thông tin trong máy tính.

Ly-thuyet-Tin-hoc-10-Canh-dieu-Bai-1-He-nhi-phan-va-ung-dung-anh-4

Ly-thuyet-Tin-hoc-10-Canh-dieu-Bai-1-He-nhi-phan-va-ung-dung-anh-5

Ly-thuyet-Tin-hoc-10-Canh-dieu-Bai-1-He-nhi-phan-va-ung-dung-anh-8

Các phép toán bit này là nền tảng cho việc thực hiện các phép tính toán và xử lý thông tin trong máy tính.